数学のおすすめの参考書ルートをわかりやすく解説します。これから数学の勉強を始める人や共通テストを使った入試を受験する人などの特に参考にしていただきたいです。使い方もあわせて解説していますので、ぜひご覧ください。
数学の特徴
数学は、理系科目の土台となる科目です。基礎を学び、定理や公式などの手札を増やしながら、その手札の組み合わせで問題にどう対処するか考えていきます。かなり地道な積み上げが大事で、時間と労力を費やさないと点数が上がらない科目なので、学習方法を考えるうえで踏まえてほしい大きなポイントが2つあります。
ポイント① ⅠA→ⅡB→ⅢCと、前に習った分野が次の分野の学習の前提となる
数学にはⅠ・A・Ⅱ・B・Ⅲ・Cの6つの分野があり、多くの入試ではⅠとA、ⅡとB、ⅢとCがセットになって出題されます(ⅡBCやⅢのみなど、例外もあり)。自分が既に学んだ手札を使いながら次の分野の内容を身につけていくので、ⅠAに穴があれば、ⅡBの難しい参考書に取り組むなどということはできません。ⅠA→ⅡB→ⅢCの順番を守ってレベルごとに学習を進めていく必要があります。
ポイント② 入試では少しひねった典型問題から複合問題が出題される
参考書では、定理や公式を学びながら問題を解いていきますが、扱う問題にも2つのレベルがあります。
典型問題:各単元の公式やパターンを組み合わせた典型的な操作で解くことができる問題。チャートなどの網羅型参考書で主に学習できる。黄チャートのコンパス1~3程度のレベル。
複合問題:異なった単元や分野の操作を組み合わせて解くことができる問題。どの公式・パターンを適用するか、問題が設定している条件から自分で考えなければいけないため、難易度があがる。黄チャートコンパス4以降程度のレベル。
問題の難易度を左右する最も大きな要因は、手札(定理や公式)の組み合わせ方がどれくらい典型のパターンから離れているか、です。典型問題の中での難易度は、計算や手続きの複雑さに由来するところが大きいですが、難しいものだとちょっとした発想が必要になることもあります。
実際に入試で出題されるのは少しひねった典型問題から複合問題であることが多いので、そのレベルに到達するためにはかなりの問題量を解けるようになる必要があります。ゼロからの発想を鍛えるというより、パターンの組み合わせ方を新しいパターンとして習得していくことで、「この解法が使えそう」と見当をつけられる範囲を広げていく作業をしていきます。
これらのポイントは、効率的に学習を進めるうえで理解しておいてほしい点です。数学の学習は短期間でどうにかなるものではありません。理系の生徒は特に分野の数も難易度も求められるため、一通り学習を終えるだけでかなりの時間がかかります。学習を始める段階である程度受験する大学・学部のレベルの目処をたて、学習計画のペースを守るか、それ以上のペースで進めることが望ましいです。
数学の問題は、与えられた条件と求めたい条件の間を、様々な操作で埋めていく作業です。簡単な問題であるほど、与えられた条件と求めたい条件までの幅が小さく、かつ教科書や参考書に公式集等で書かれているような簡単な作業で埋めることができます。一方難問では、この幅が大きく、小問でところどころチェックポイントを設定し、各地点まで辿り着ける人をふるい分けています。
演習に移行するまでの参考書では、この幅を埋めるために必要な操作を一つ一つ身につけることを意識して取り組んでください。
数学の学習について
文系の生徒はI→A→Ⅱ→B→Cの順に、理系の生徒はⅠ→A→Ⅱ→B→Ⅲ→Cの順に学習を進めていきます。二次試験の範囲として数B「統計的な推測」を外す大学も多い中、出願者の多い国公立大学が範囲に含めていることもあります。年度、学部ごとに出題範囲が異なる大学もあるため、志望校を決める際には出題範囲をよく確認しておきましょう。
また、大学によって解答方法が記述式やマーク式などと異なります。記述式では論理の正確性が、マーク式ではスピードと計算の正確性が求められるなど、対策すべきポイントが変わってくるのでその点にも注意して受験大学を選び、対策していきましょう。
数学の共通テストについて
◎ⅠA 出題範囲
必答(第一問・第二問・第三問・第四問):数と式、二次関数、図形と計量やデータの分析、場合の数・確率、図形の性質
◎ⅡBC 出題範囲
必答(第一問・第二問・第三問):三角関数、指数・対数、微分積分の考え
選択(第四問・第五問・第六問・第七問):統計的な推測、数列、ベクトル、平面上の曲線と複素数平面から3問選択
センター試験から共通テストに移行する段階で、出題が数学の知識や典型問題の解き方を問う内容から、問題解決の手段としての数学を重視する内容へと変更されてきました。これにより問題文中では具体的な問題を設定し、公式やパターンを使って解いていく過程を穴埋めとして問われるようになりました。普段の学習から一つ一つの公式に対し、ただ暗記をするのではなく、どうしてその公式が導かれるのかや、その公式の意味などの理解が必要になります。特に数学ⅡBは解答時間が10分増えたものの、解答すべき大問が2問増えました。制限時間がさらに厳しい試験となったため、計算スピードが求められるだけでなく、問題の状況や誘導の意図を素早く理解する力が求められています。
★模試などで共通テスト形式のものを解いた際は、自分が点数を落とす原因をよく分析すること!!
「数学の特徴」で説明したように、数学は積み重ねです。極端な話、点数が取れなかった原因がその分野の学習にあるとは限りません。分野ごとの復習も重要ですが、自分がどんな時にミスをするのか、どの操作が求められている状況に気づけないのか、間違え方の癖を分析しましょう
また、共通テストは問題の誘導が少し独特です。基本的に、問題を解く過程を穴埋めするような形で出題されますが、今どのような道筋で解いているのか、文章でのガイドはほとんどありません。この道筋を読み取れる生徒はすらすらと解いていくことができる一方、求められている操作がわからない生徒は遠回りな操作をしてしまいます。その結果、時間を浪費し、想定よりも点数が伸びないという状況に陥ります。
各単元の学習が進んでいない段階では、各操作の意味をきちんと理解することでこのような状況を回避することができます。根本的な解決を図るには時間が足りない場合、とにかく演習量でカバーし、スピードを上げることでなんとか点数を伸ばしましょう。模試などの結果から間違え方の癖を分析した時、その原因が独特な誘導に乗れていないことにあるときは直前期から対策を行うのではなく、共通テスト形式の参考書などで、誘導や共通テストの形式になれるための対策を早めに行うようにしましょう。
ルート種別

どの到達レベルの生徒でも、基本は同じ参考書を通過(当然カスタムすることもあるが、軸は同じ)。ランクを上げる=参考書を追加する。主要科目など、時間をかけて基礎に穴がないように固めていく科目に多い。
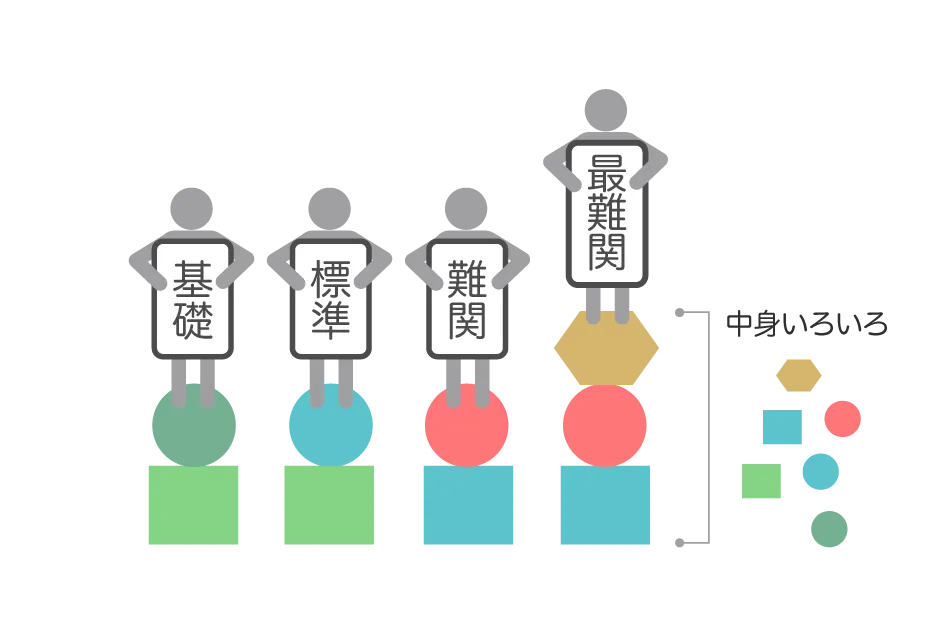
到達レベルによって、使用する参考書の組み合わせが異なる。ランクを上げる=参考書がそもそも異なる。副教科など、参考書の種類が多く(理解本・資料集・まとめ本・演習用問題集・一問一答…など)、なるべく少ない参考書数で効率よく終わらせたい科目に多い。
※これら2つの考え方を、同じ科目内で両方使うことも多い。最初に使うインプットの数冊はセット方式、問題集は積み上げ方式、など。
★数学では、最短距離の積み上げ方式を採用★
他塾ルートに比べ圧倒的に冊数が少なく、最低の冊数を完璧に仕上げることで合格を目指すルートです。数学の参考書は、1冊の参考書ですべての範囲をまんべんなく網羅できるよう構成されています。そのため、様々な参考書に手を出すよりも1冊ずつ完璧に仕上げるほうが最終的な完成度が上がる、という考え方に基づいて編成しました。また、受験まで時間が限られている場合、逆転合格よりも確実に行ける大学を目指せる構成となっており、目標の大学を狙い撃ちすることができる現実的な学習計画になっています。
数学MAP
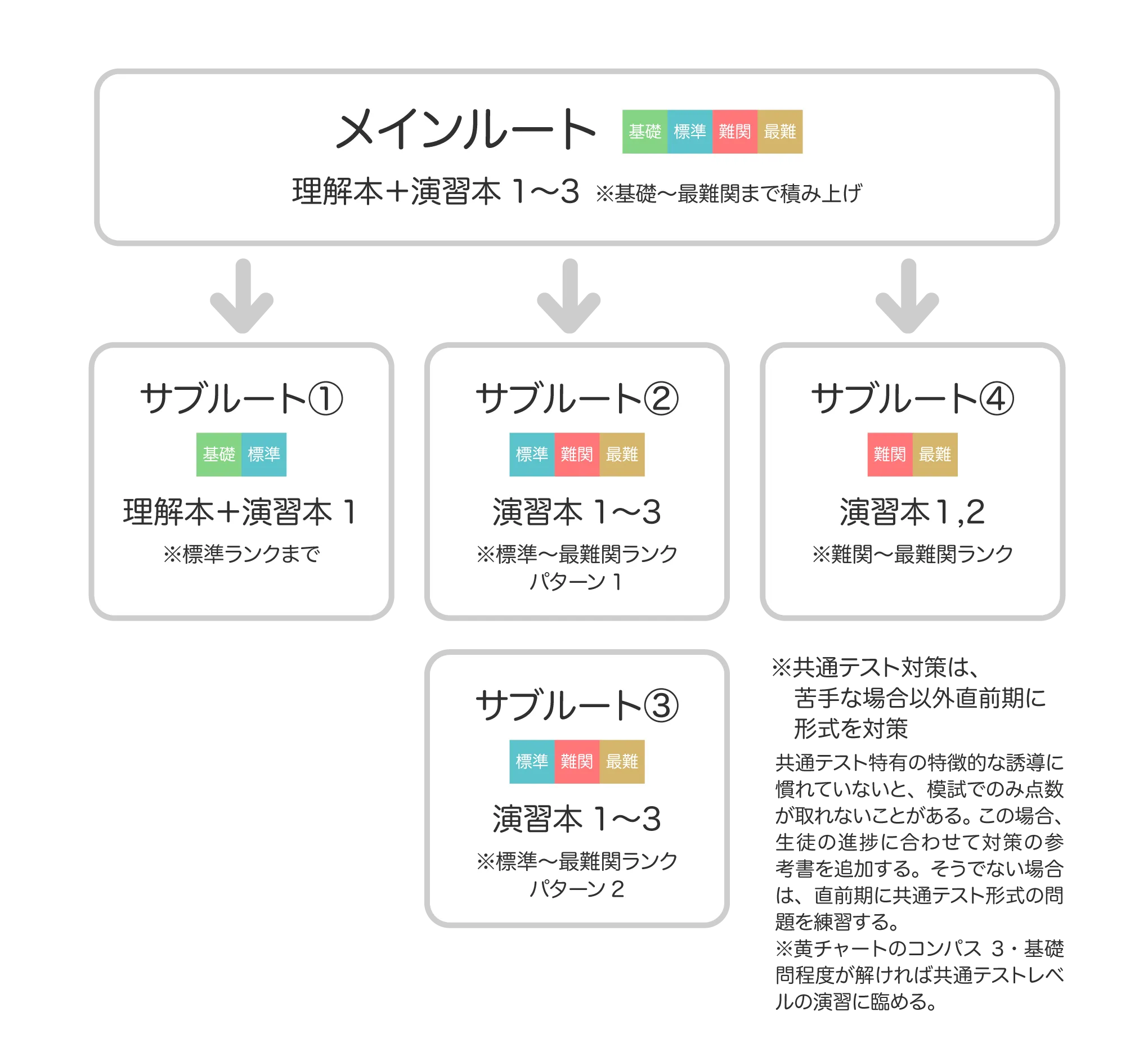
ルートの選び方 〜目標ランクの設定について〜
とにかく学習に時間がかかるので、初めに現在のランクと目標とするランクをなるべく確定させることが重要です。特に目標とするランクは、無駄に難しい問題を解かせて時間を浪費させることがないよう、残り時間を考慮してかなり慎重に選びましょう。もちろん途中でランクを下げたり上げたりすることも可能ではあり、一旦現実的な範囲で目指せば、ランクを途中で上げても長い時間をかけすぎず、難しい問題に挑戦することができます。ランクを変更する可能性があるかも含めて、ルートを選ぶようにしてください。
★最難関ランクの上位レベルまで到達するためには、多くの工夫と時間、演習量が必要です。他科目との兼ね合いを考慮しても、一問一問丁寧に取り組むほど数学に時間を割けること、入試まであと1年くらいの時点で難関ランクの参考書の問題が解けるレベルであることが理想的です。ただし、学校での学習状況や勉強方法で挽回することもできます。順当に学習していけば到達できるペースとどれくらい距離があるのか意識しながら計画的に学習しましょう。
※文系数学について※
ルート参考書に「◆文」の記載がある参考書をピックアップして学習してください。なお、『やさしい高校数学』シリーズや、黄チャート、青チャートはⅢCが掲載されていますが、Cのみの参考書が出版されているためそちらを使用するのがおすすめです。ⅢCのC部分とCのみの参考書は内容が同じであるため、参考書の使い方ページはⅢCのものを参照しください。なお、『基礎問題精講』シリーズ、『標準問題精講』シリーズなどはⅡBにベクトルが含まれたものをルートに選定しているので、別でCを学習する必要はありません。
目標ランクごとの学習ポイント
①標準ランクまでを目指す場合
完全に覚えて、とにかく何も考えずに操作できるまで問題を繰り返し解きます。パターン学習で構わないので標準ランクまでの参考書の問題が完璧に解けるようになるまで、また、解答の要素を落とさないですべてかけるようになるまで繰り返します。一問一問時間をかけて考え込む必要はありません。
②難関ランクを目指す場合
一つ一つの作業の意味を理解することが必要になってきます。受験勉強の開始時点で受験まで時間があり、学校での分野の学習が進んでいない場合は、一つ一つの操作の意味を参考書の解答に書き込むなどして理解を深め、一問に時間をかけて取り組むことができれば数学で合格点を狙うことができます。一方、受験勉強の開始時点である程度学校での学習が進んでおり、受験まで時間がない場合は、解ける問題を確実に取るという方針で進めます。意味を考えるより量をこなし、他教科の足を引っ張らない程度の完成度で合格点を狙うのが現実的です。
③最難関ランクを目指す場合
難関ランクの上位にいる場合、最難関ランクの問題にとにかく触れ、操作を始める前の「実験」(条件を満たす解をまず探す段階)の経験値を上げることを目指しましょう。具体的には、黄チャートのコンパス4・5以上の問題では、問題を見てすぐに方針が浮かび解き始める、ということは難しくなります。そのような問題ではノートの見開き1ページを1問に使い、左ページに計算や実験の過程を残し、右ページに解答を書く練習をすると、採点をして解答を見直す際にも思考の流れが確認でき良いでしょう。
メインルート
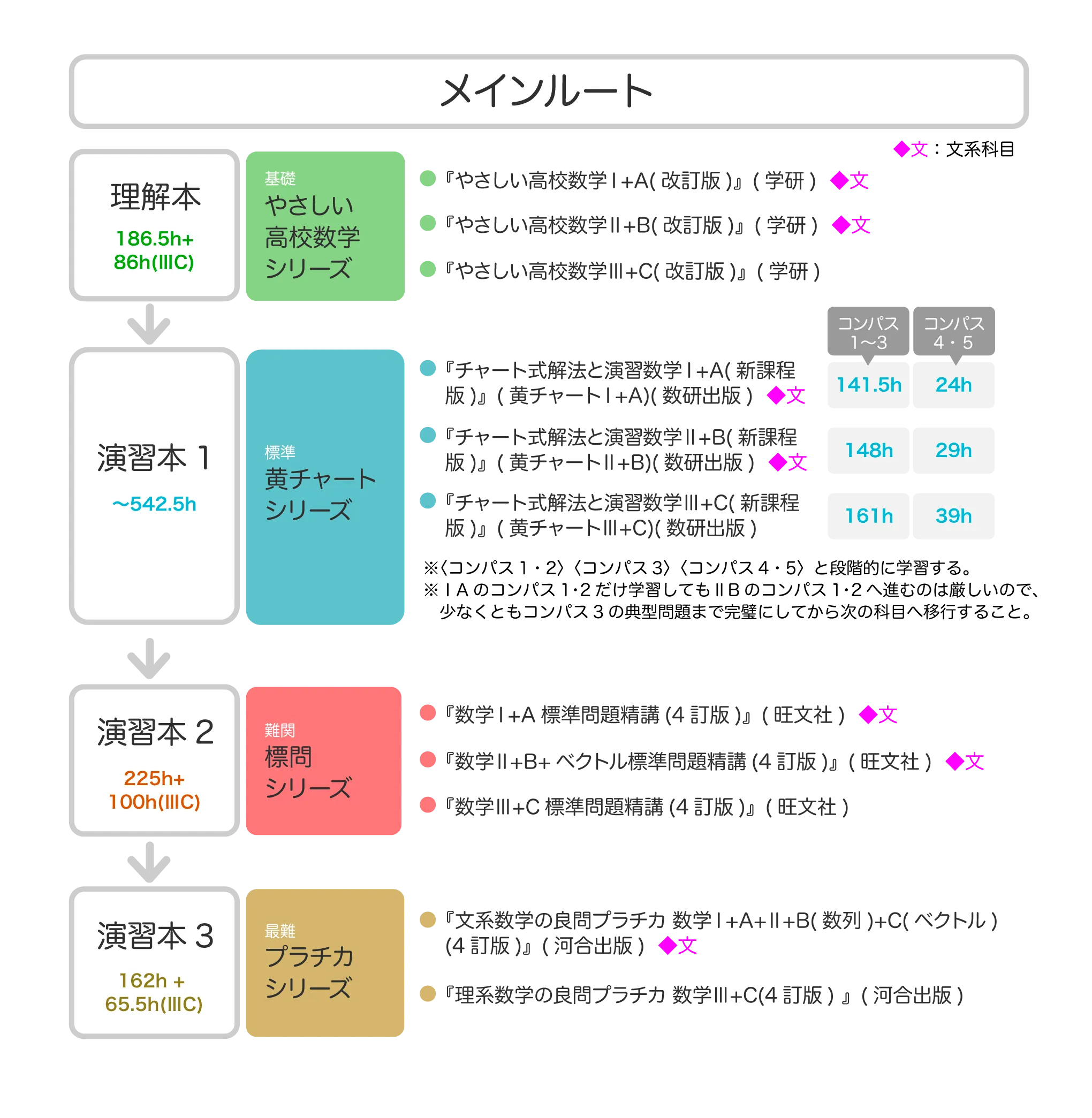
【所要時間】88.5h ①理解本 ②本書は基礎中の基礎から、会話調で非常になじみやすく、かつ分かりやすく誰でも理解できるレベルで説明されているという理由から、初学者や、学校の授業内容に不安がある生徒向けに採用しました。例えば、式の展開の分野では、展開のための計算の順序を矢印を踏まえて行われており、視覚的にも読み取りやすいでしょう。このような特徴のある本書は基礎から学ぶ1冊目に最適です。 ③本書は問題を解くための道具を知る段階にあるので、力をつけるには本書で時間をかけすぎず、演習本で問題を解く段階に早く移るようにしましょう。また、すでに学習をある程度進めている人にとっては本書がやさしく感じる場合もあるでしょう。その場合には『チャート式解法と演習(新課程版)』シリーズ(黄チャート)から始めるとよいでしょう。
参考書の使い方はこちら
【所要時間】98h ①理解本 ②本書は基礎中の基礎から、会話調で非常になじみやすく、かつ分かりやすく誰でも理解できるレベルで説明されているという理由から、初学者や、学校の授業内容に不安がある生徒向けに採用しました。例えば、不等式の表す領域の単元では、色別で図を分けており、視覚的にも読み取りやすくなっています。このような特徴のある本書は基礎から学ぶ1冊目に最適です。 ③本書は問題を解くための道具を知る段階にあるので、力をつけるには本書で時間をかけすぎず、演習本で問題を解く段階に早く移るようにしましょう。また、すでに学習をある程度進めている人にとっては本書がやさしく感じる場合もあるでしょう。その場合には『チャート式解法と演習(新課程版)』シリーズ(黄チャート)から始めるとよいでしょう。
参考書の使い方はこちら
【所要時間】86h ①理解本 ②本書は基礎中の基礎から、会話調で非常になじみやすく、かつ分かりやすく誰でも理解できるレベルで説明されているという理由から、初学者や、学校の授業内容に不安がある生徒向けに採用しました。例えば、「いろいろな関数」の単元では、グラフの形の特徴などを細かく解説しており、初学者にとっては非常にとっかかりやすくなっています。このような特徴のある本書は基礎から学ぶ1冊目に最適です。 ③数学Ⅲでは基礎計算の正確性が重要であるので、急いでハイレベルな問題集に進むことなく、他の参考書を併用しながら計算練習を積み、正確に計算が合わせられるようにしましょう。また、すでに学習をある程度進めている人にとっては本書がやさしく感じる場合もあるでしょう。その場合には『チャート式解法と演習(新課程版)』シリーズ(黄チャート)から始めるとよいでしょう。
参考書の使い方はこちら
【所要時間】77h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス1・2は、『やさしい高校数学(改訂版)』シリーズや授業等で学んだ、基本的な数学操作の練習を行う段階であり、細かな式変形にはきちんと注釈も乗っていて疑問を残さず演習を行いやすいという理由から『やさしい高校数学(改訂版)』シリーズで学んだ内容の演習が必要な生徒向けに採用しました。コンパス1・2では、たくさんの計算練習を行い計算スピードを上げ、勝手に手が動くくらいの速さで計算できるよう解いていきます。 ③コンパス3以降の典型問題の学習に時間がかかるので、この範囲は素早く終わらせることを意識しましょう。時間に余裕がなく、本書で解くような範囲はマスターしている生徒はコンパス3から取り組んでも構いません。しかし、この範囲は理解していることと、できるようになっていることを誤認しやすい範囲でもあるので、自分の状況をよく把握し、苦手意識のある分野は積極的に活用するとよいでしょう。
【所要時間】64.5h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。難関大の問題に直結する内容を多く含む構成であるため、典型問題をマスターすることを目指す生徒向けに採用しました。コンパス3は、すべての典型問題を反射で解答できるようになるために繰り返し演習する教材として最適です。 ③理解できていても、実際に取り組んでみると案外最後まで完璧に解ききることが難しい範囲であるので、どんな問題のどこで詰まってしまうのかをきちんと把握することが重要です。このレベルの基礎を固めなければ、難関ランク以上の問題を解くことが難しくなります。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】24h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。初歩の応用問題で、入試本番で挑むような問題への基礎力をつけたい生徒向けに採用しました。文字を含んだり置き換えを用いたりと、高い思考力を要求する問題では、すぐに解答を見ず、自ら調べながらよく思考することで飛躍的なレベルアップを目指します。 ③すぐに答えを見ずよく思考し、なぜその作業で解答にたどり着けるのかを考えながら演習に取り組むことが重要です。また、解答の論理関係(必要十分条件)等にもよく注意しながら解答を書くようにしましょう。コンパス3から飛躍的に難易度が上がっているので、確実にコンパス3を固めてから取り組むことにも注意が必要です。
【所要時間】87h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス1・2は、『やさしい高校数学(改訂版)』シリーズや授業等で学んだ、基本的な数学操作の練習を行う段階であり、細かな式変形にはきちんと注釈も乗っていて疑問を残さず演習を行いやすいという理由から『やさしい高校数学(改訂版)』シリーズで学んだ内容の演習が必要な生徒向けに採用しました。コンパス1・2では、たくさんの計算練習を行い計算スピードを上げ、勝手に手が動くくらいの速さで計算できるよう解いていきます。 ③コンパス3以降の典型問題の学習に時間がかかるので、この範囲は素早く終わらせることを意識しましょう。時間に余裕がなく、本書で解くような範囲はマスターしている生徒はコンパス3から取り組んでも構いません。しかし、この範囲は理解していることと、できるようになっていることを誤認しやすい範囲でもあるので、自分の状況をよく把握し、苦手意識のある分野は積極的に活用するとよいでしょう。
【所要時間】61h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。難関大の問題に直結する内容を多く含む構成であるため、典型問題をマスターすることを目指す生徒向けに採用しました。コンパス3は、すべての典型問題を反射で解答できるようになるために繰り返し演習する教材として最適です。 ③理解できていても、実際に取り組んでみると案外最後まで完璧に解ききることが難しい範囲であるので、どんな問題のどこで詰まってしまうのかをきちんと把握することが重要です。このレベルの基礎を固めなければ、難関ランク以上の問題を解くことが難しくなります。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】29h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。初歩の応用問題で、入試本番で挑むような問題への基礎力をつけたい生徒向けに採用しました。文字を含んだり置き換えを用いたりと、高い思考力を要求する問題では、すぐに解答を見ず、自ら調べながらよく思考することで飛躍的なレベルアップを目指します。 ③すぐに答えを見ずよく思考し、なぜその作業で解答にたどり着けるのかを考えながら演習に取り組むことが重要です。また、解答の論理関係(必要十分条件)等にもよく注意しながら解答を書くようにしましょう。コンパス3から飛躍的に難易度が上がっているので、確実にコンパス3を固めてから取り組むことにも注意が必要です。
参考書の使い方はこちら
【所要時間】92.5h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス1・2は、『やさしい高校数学(改訂版)』シリーズや授業等で学んだ、基本的な数学操作の練習を行う段階であり、細かな式変形にはきちんと注釈も乗っていて疑問を残さず演習を行いやすいという理由から『やさしい高校数学(改訂版)』シリーズで学んだ内容の演習が必要な生徒向けに採用しました。コンパス1・2では、たくさんの計算練習を行い計算スピードを上げ、勝手に手が動くくらいの速さで計算できるよう解いていきます。 ③コンパス3以降の典型問題の学習に時間がかかるので、この範囲は素早く終わらせることを意識しましょう。時間に余裕がなく、本書で解くような範囲はマスターしている生徒はコンパス3から取り組んでも構いません。しかし、この範囲は理解していることと、できるようになっていることを誤認しやすい範囲でもあるので、自分の状況をよく把握し、苦手意識のある分野は積極的に活用するとよいでしょう。
【所要時間】68.5h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。難関大の問題に直結する内容を多く含む構成であるため、典型問題をマスターすることを目指す生徒向けに採用しました。コンパス3は、すべての典型問題を反射で解答できるようになるために繰り返し演習する教材として最適です。 ③理解できていても、実際に取り組んでみると案外最後まで完璧に解ききることが難しい範囲であるので、どんな問題のどこで詰まってしまうのかをきちんと把握することが重要です。このレベルの基礎を固めなければ、難関ランク以上の問題を解くことが難しくなります。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】39h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。初歩の応用問題で、入試本番で挑むような問題への基礎力をつけたい生徒向けに採用しました。文字を含んだり置き換えを用いたりと、高い思考力を要求する問題では、すぐに解答を見ず、自ら調べながらよく思考することで飛躍的なレベルアップを目指します。 ③すぐに答えを見ずよく思考し、なぜその作業で解答にたどり着けるのかを考えながら演習に取り組むことが重要です。また、解答の論理関係(必要十分条件)等にもよく注意しながら解答を書くようにしましょう。コンパス3から飛躍的に難易度が上がっているので、確実にコンパス3を固めてから取り組むことにも注意が必要です。
【所要時間】88.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】136.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】100h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】162h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。過去問演習前に最難関大学の問題の解法の思考の経験を積むことができるため、最難関ランクの大学で数学を武器にして安定的に合格を狙いたい人向けに採用しました。本書以前に学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学受験の総仕上げとして最適な一冊です。 ③問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。本書は見たことがない解法や問題を経験しておく、ということが目的であるので時間をかけすぎず、他の教科とのバランスを考えながら取り組みましょう。また、本書はレベルが高いため、特に文系の生徒はこの参考書の学習自体が志望大学の合格に必要なのかよく検討してから学習を始めましょう。
【所要時間】65.5h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。本改訂により新課程のⅢCに対応し、過去問演習前に最難関大学の問題の解法の思考を十分に練習できる内容となっており、最難関ランクの大学で数学を武器として安定的に合格を狙いたい人向けに採用しました。これまでに学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学の受験の総仕上げとして最適です。最難関ランクの大学の理系の問題では数ⅢCの範囲が合否を分けるので、本書を身につけることができれば数学では確実に合格圏に入ることができるでしょう。 ③本書は理系の最難関レベルの大学を志望する生徒が取り組むので、『文系数学の良問プラチカ』とは違い、標問と同じくらいの練度で取り組みましょう。問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。
サブルート(メインルートから分岐)
①標準ランクまでを目標にする生徒のためのルート〜535.5h

【所要時間】88.5h ①理解本 ②本書は基礎中の基礎から、会話調で非常になじみやすく、かつ分かりやすく誰でも理解できるレベルで説明されているという理由から、初学者や、学校の授業内容に不安がある生徒向けに採用しました。例えば、式の展開の分野では、展開のための計算の順序を矢印を踏まえて行われており、視覚的にも読み取りやすいでしょう。このような特徴のある本書は基礎から学ぶ1冊目に最適です。 ③本書は問題を解くための道具を知る段階にあるので、力をつけるには本書で時間をかけすぎず、演習本で問題を解く段階に早く移るようにしましょう。標準ランクを目指す場合は、本書で基礎を十分理解した後、『基礎問題精講』に進み、典型問題を確実にマスターするようにしましょう。
【所要時間】98h ①理解本 ②本書は基礎中の基礎から、会話調で非常になじみやすく、かつ分かりやすく誰でも理解できるレベルで説明されているという理由から、初学者や、学校の授業内容に不安がある生徒向けに採用しました。例えば、不等式の表す領域の単元では、色別で図を分けており、視覚的にも読み取りやすくなっています。このような特徴のある本書は基礎から学ぶ1冊目に最適です。 ③本書は問題を解くための道具を知る段階にあるので、力をつけるには本書で時間をかけすぎず、演習本で問題を解く段階に早く移るようにしましょう。標準ランクを目指す場合は、本書で基礎を十分理解した後、『基礎問題精講』に進み、典型問題を確実にマスターするようにしましょう。
【所要時間】86h ①理解本 ②本書は基礎中の基礎から、会話調で非常になじみやすく、かつ分かりやすく誰でも理解できるレベルで説明されているという理由から、初学者や、学校の授業内容に不安がある生徒向けに採用しました。例えば、「いろいろな関数」の単元では、グラフの形の特徴などを細かく解説しており、初学者にとっては非常にとっかかりやすくなっています。このような特徴のある本書は基礎から学ぶ1冊目に最適です。 ③数学Ⅲでは基礎計算の正確性が重要であるので、急いでハイレベルな問題集に進むことなく、他の参考書を併用しながら計算練習を積み、正確に計算が合わせられるようにしましょう。標準ランクを目指す場合は、本書で基礎を十分理解した後、『基礎問題精講』に進み、典型問題を確実にマスターするようにしましょう。
【所要時間】82h ①演習本 ②本書は基本的な問題の必要最低限の出題パターンを、短時間で網羅できる参考書です。タイパよく、典型題のパターンを明解な解説と共に学習できるため、短時間で基礎ランクを目指したい生徒向けに採用しました。各問題の「ポイント」や「精講」では解法の指針が簡単にまとめられており、疑問を残さず学習することができます。『やさしい高校数学』で覚えた公式を短時間で実際に使えるようにするための演習に最適な一冊です。 ③チャートと比較して網羅性が低いため、典型題のパターンが足りておらず、難関レベル以上の大学の問題に完璧に対応することは難しいでしょう。また、本書と『標準問題精講』のレベルの差が大きいため、接続が難しいので、ルート選択の前によく志望校を検討しましょう。
【所要時間】104h ①演習本 ②本書は基本的な問題の必要最低限の出題パターンを、短時間で網羅できる参考書です。タイパよく、典型題のパターンを明解な解説と共に学習できるため、短時間で基礎ランクを目指したい生徒向けに採用しました。各問題の「ポイント」や「精講」では解法の指針が簡単にまとめられており、疑問を残さず学習することができます。『やさしい高校数学』で覚えた公式を短時間で実際に使えるようにするための演習に最適な一冊です。 ③チャートと比較して網羅性が低いため、典型題のパターンが足りておらず、難関レベル以上の大学の問題に完璧に対応することは難しいでしょう。また、本書と『標準問題精講』のレベルの差が大きいため、接続が難しいので、ルート選択の前によく志望校を検討しましょう。
【所要時間】77h ①演習本 ②本書は基本的な問題の必要最低限の出題パターンを、短時間で網羅できる参考書です。タイパよく、典型題のパターンを明解な解説と共に学習できるため、短時間で基礎ランクを目指したい生徒向けに採用しました。各問題の「ポイント」や「精講」では解法の指針が簡単にまとめられており、疑問を残さず学習することができます。『やさしい高校数学』で覚えた公式を短時間で実際に使えるようにするための演習に最適な一冊です。 ③チャートと比較して網羅性が低いため、典型題のパターンが足りておらず、難関レベル以上の大学の問題に完璧に対応することは難しいでしょう。また、本書と『標準問題精講』のレベルの差が大きいため、接続が難しいので、ルート選択の前によく志望校を検討しましょう。
②標準ランクから最難関ランクを目指す人のための時短ルート1〜773h
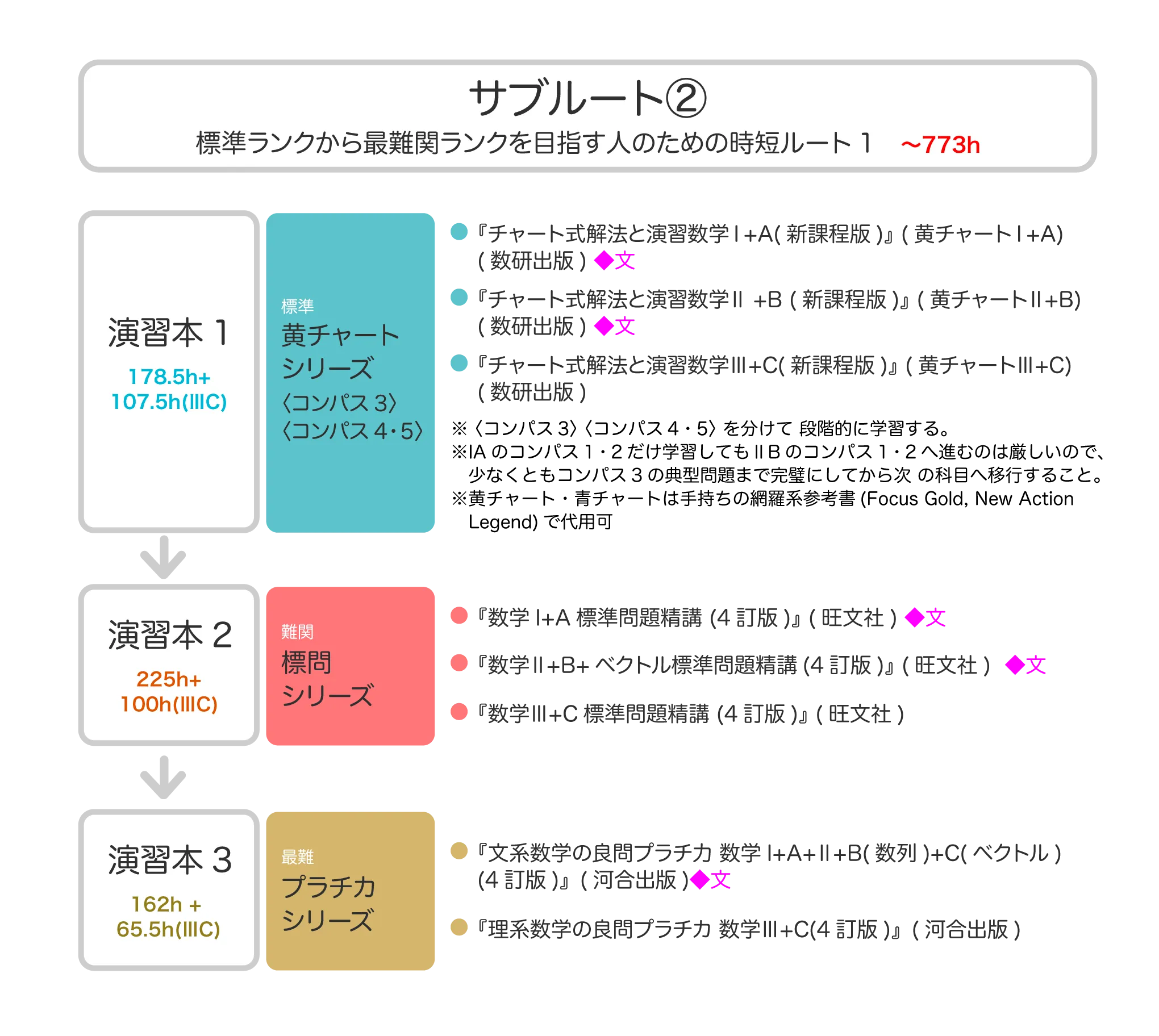
【所要時間】64.5h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。難関大の問題に直結する内容を多く含む構成であるため、典型問題をマスターすることを目指す生徒向けに採用しました。コンパス3は、すべての典型問題を反射で解答できるようになるために繰り返し演習する教材として最適です。 ③理解できていても、実際に取り組んでみると案外最後まで完璧に解ききることが難しい範囲であるので、どんな問題のどこで詰まってしまうのかをきちんと把握することが重要です。このレベルの基礎を固めなければ、難関ランク以上の問題を解くことが難しくなります。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】24h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。初歩の応用問題で、入試本番で挑むような問題への基礎力をつけたい生徒向けに採用しました。文字を含んだり置き換えを用いたりと、高い思考力を要求する問題では、すぐに解答を見ず、自ら調べながらよく思考することで飛躍的なレベルアップを目指します。 ③すぐに答えを見ずよく思考し、なぜその作業で解答にたどり着けるのかを考えながら演習に取り組むことが重要です。また、解答の論理関係(必要十分条件)等にもよく注意しながら解答を書くようにしましょう。コンパス3から飛躍的に難易度が上がっているので、確実にコンパス3を固めてから取り組むことにも注意が必要です。
【所要時間】61h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。難関大の問題に直結する内容を多く含む構成であるため、典型問題をマスターすることを目指す生徒向けに採用しました。コンパス3は、すべての典型問題を反射で解答できるようになるために繰り返し演習する教材として最適です。 ③理解できていても、実際に取り組んでみると案外最後まで完璧に解ききることが難しい範囲であるので、どんな問題のどこで詰まってしまうのかをきちんと把握することが重要です。このレベルの基礎を固めなければ、難関ランク以上の問題を解くことが難しくなります。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】29h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。初歩の応用問題で、入試本番で挑むような問題への基礎力をつけたい生徒向けに採用しました。文字を含んだり置き換えを用いたりと、高い思考力を要求する問題では、すぐに解答を見ず、自ら調べながらよく思考することで飛躍的なレベルアップを目指します。 ③すぐに答えを見ずよく思考し、なぜその作業で解答にたどり着けるのかを考えながら演習に取り組むことが重要です。また、解答の論理関係(必要十分条件)等にもよく注意しながら解答を書くようにしましょう。コンパス3から飛躍的に難易度が上がっているので、確実にコンパス3を固めてから取り組むことにも注意が必要です。
参考書の使い方はこちら
【所要時間】68.5h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も幅広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。難関大の問題に直結する内容を多く含む構成であるため、典型問題をマスターすることを目指す生徒向けに採用しました。コンパス3は、すべての典型問題を反射で解答できるようになるために繰り返し演習する教材として最適です。 ③理解できていても、実際に取り組んでみると案外最後まで完璧に解ききることが難しい範囲であるので、どんな問題のどこで詰まってしまうのかをきちんと把握することが重要です。このレベルの基礎を固めなければ、難関ランク以上の問題を解くことが難しくなります。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】39h ①演習本 ②本書は網羅性が高く、網羅型参考書としては最も広いレベル帯の生徒が使える参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。初歩の応用問題で、入試本番で挑むような問題への基礎力をつけたい生徒向けに採用しました。文字を含んだり置き換えを用いたりと、高い思考力を要求する問題では、すぐに解答を見ず、自ら調べながらよく思考することで飛躍的なレベルアップを目指します。 ③すぐに答えを見ずよく思考し、なぜその作業で解答にたどり着けるのかを考えながら演習に取り組むことが重要です。また、解答の論理関係(必要十分条件)等にもよく注意しながら解答を書くようにしましょう。コンパス3から飛躍的に難易度が上がっているので、確実にコンパス3を固めてから取り組むことにも注意が必要です。
【所要時間】88.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】136.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】100h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】162h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。過去問演習前に最難関大学の問題の解法の思考の経験を積むことができるため、最難関ランクの大学で数学を武器にして安定的に合格を狙いたい人向けに採用しました。本書以前に学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学受験の総仕上げとして最適な一冊です。 ③問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。本書は見たことがない解法や問題を経験しておく、ということが目的であるので時間をかけすぎず、他の教科とのバランスを考えながら取り組みましょう。また、本書はレベルが高いため、特に文系の生徒はこの参考書の学習自体が志望大学の合格に必要なのかよく検討してから学習を始めましょう。
【所要時間】65.5h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。本改訂により新課程のⅢCに対応し、過去問演習前に最難関大学の問題の解法の思考を十分に練習できる内容となっており、最難関ランクの大学で数学を武器として安定的に合格を狙いたい人向けに採用しました。これまでに学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学の受験の総仕上げとして最適です。最難関ランクの大学の理系の問題では数ⅢCの範囲が合否を分けるので、本書を身につけることができれば数学では確実に合格圏に入ることができるでしょう。 ③本書は理系の最難関レベルの大学を志望する生徒が取り組むので、『文系数学の良問プラチカ』とは違い、標問と同じくらいの練度で取り組みましょう。問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。
③標準ランクから最難関ランクを目指す人のための時短ルート2〜802.5h
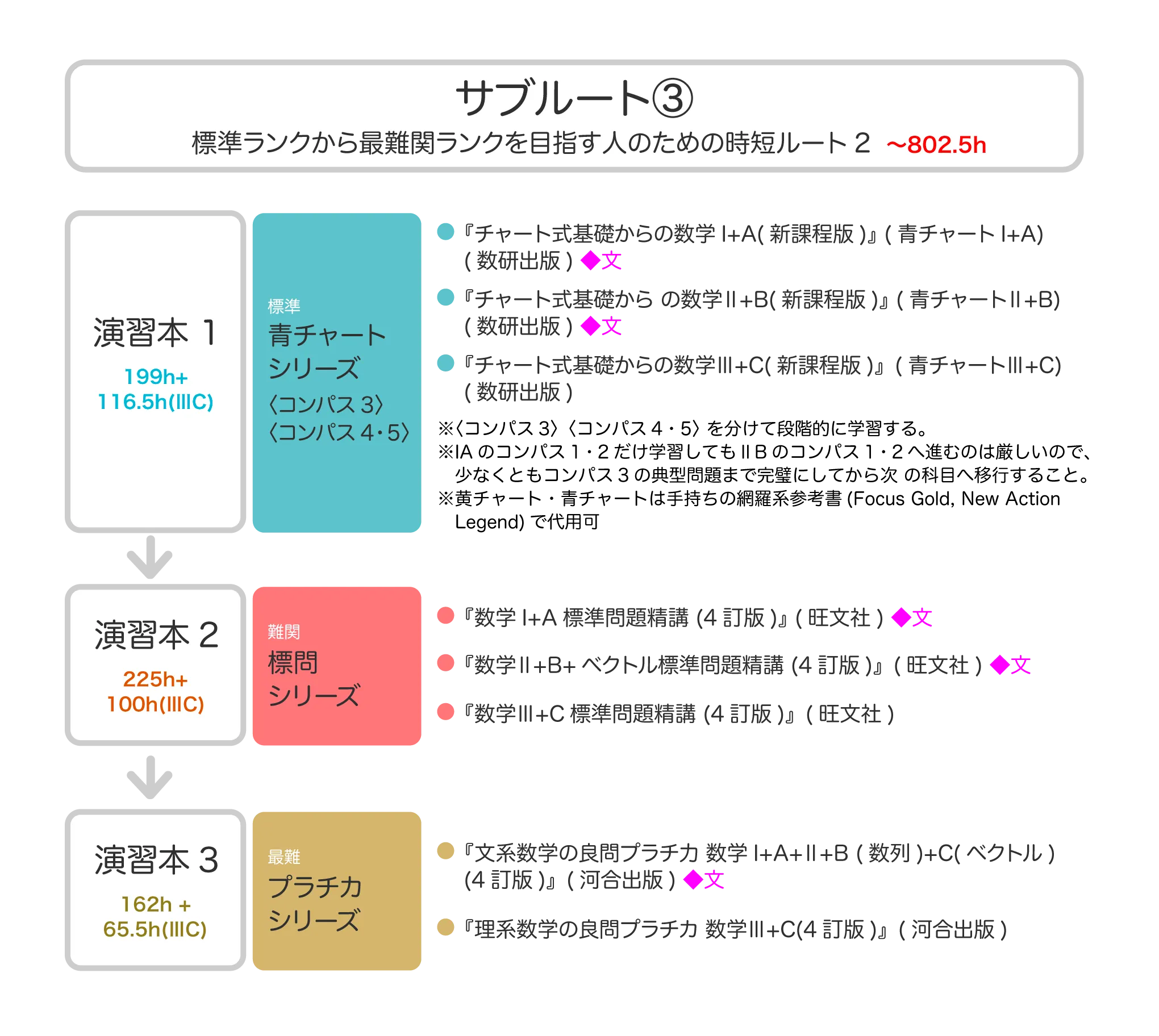
【所要時間】73.5h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。基本例題に加え重要例題も掲載しており、難関大の問題に直結する内容を多く含む構成であるため、典型題を身につけつつ難関大を視野に入れた学習をする生徒向けに採用しました。実際の入試問題で問われる形の典型題を多く収録しているため、典型題に加え、初見の問題に対しどのような思考をして取り組めばよいのか、練習をするのに最適な一冊です。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】22.5h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。実際の難関大の入試問題に触れ、公式や操作の理由をきちんと考えて理解することで、飛躍的な数学力の向上を目指す生徒向けに採用しました。入試問題での問われ方や解法に触れることで、その後の参考書で、ポイントをついた解答の作成や問われやすいパターンの学習がスムーズになるでしょう。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。青チャートのコンパス4・5はかなりレベルが高いため、初めて問題を解く際はどうしても答えを見てしまうことが多くなってしまいますが、解答の暗記はあまり意味がないので、どうして問題文を読んでこの解答にたどり着くのか、思考の過程をよく検討することや数学的な操作の意味を常に理解しながら取り組むことが重要です。
【所要時間】69h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。基本例題に加え重要例題も掲載しており、難関大の問題に直結する内容を多く含む構成であるため、典型題を身につけつつ難関大を視野に入れた学習をする生徒向けに採用しました。実際の入試問題で問われる形の典型題を多く収録しているため、典型題に加え、初見の問題に対しどのような思考をして取り組めばよいのか、練習をするのに最適な一冊です。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】34h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。実際の難関大の入試問題に触れ、公式や操作の理由をきちんと考えて理解することで、飛躍的な数学力の向上を目指す生徒向けに採用しました。入試問題での問われ方や解法に触れることで、その後の参考書で、ポイントをついた解答の作成や問われやすいパターンの学習がスムーズになるでしょう。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。青チャートのコンパス4・5はかなりレベルが高いため、初めて問題を解く際はどうしても答えを見てしまうことが多くなってしまいますが、解答の暗記はあまり意味がないので、どうして問題文を読んでこの解答にたどり着くのか、思考の過程をよく検討することや数学的な操作の意味を常に理解しながら取り組むことが重要です。
【所要時間】77h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。基本例題に加え重要例題も掲載しており、難関大の問題に直結する内容を多く含む構成であるため、典型題を身につけつつ難関大を視野に入れた学習をする生徒向けに採用しました。実際の入試問題で問われる形の典型題を多く収録しているため、典型題に加え、初見の問題に対しどのような思考をして取り組めばよいのか、練習をするのに最適な一冊です。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】39.5h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。実際の難関大の入試問題に触れ、公式や操作の理由をきちんと考えて理解することで、飛躍的な数学力の向上を目指す生徒向けに採用しました。入試問題での問われ方や解法に触れることで、その後の参考書で、ポイントをついた解答の作成や問われやすいパターンの学習がスムーズになるでしょう。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。青チャートのコンパス4・5はかなりレベルが高いため、初めて問題を解く際はどうしても答えを見てしまうことが多くなってしまいますが、解答の暗記はあまり意味がないので、どうして問題文を読んでこの解答にたどり着くのか、思考の過程をよく検討することや数学的な操作の意味を常に理解しながら取り組むことが重要です。
【所要時間】88.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】136.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】100h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】162h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。過去問演習前に最難関大学の問題の解法の思考の経験を積むことができるため、最難関ランクの大学で数学を武器にして安定的に合格を狙いたい人向けに採用しました。本書以前に学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学受験の総仕上げとして最適な一冊です。 ③問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。本書は見たことがない解法や問題を経験しておく、ということが目的であるので時間をかけすぎず、他の教科とのバランスを考えながら取り組みましょう。また、本書はレベルが高いため、特に文系の生徒はこの参考書の学習自体が志望大学の合格に必要なのかよく検討してから学習を始めましょう。
【所要時間】65.5h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。本改訂により新課程のⅢCに対応し、過去問演習前に最難関大学の問題の解法の思考を十分に練習できる内容となっており、最難関ランクの大学で数学を武器として安定的に合格を狙いたい人向けに採用しました。これまでに学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学の受験の総仕上げとして最適です。最難関ランクの大学の理系の問題では数ⅢCの範囲が合否を分けるので、本書を身につけることができれば数学では確実に合格圏に入ることができるでしょう。 ③本書は理系の最難関レベルの大学を志望する生徒が取り組むので、『文系数学の良問プラチカ』とは違い、標問と同じくらいの練度で取り組みましょう。問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。
④難関ランク・最難関ランクからの人のためのルート〜487h

【所要時間】88.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】136.5h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】100h ①演習本 ②本書は高い思考力を要求する問題が多く掲載されている、非常に難易度の高い問題集です。丁寧な解説があることから、時間をかけて最難関ランクの問題演習に繋がる力を身につけることを目指す生徒向けに採用しました。各問題についている「精講」とよばれるパートで基本事項から振り返ることができるため、高難易度の問題での新たな考え方を理解し、ストックを増やすのに最適な一冊です。 ③式変形が常に同値であるかを確認しながら解くことを意識し、実際の試験で減点されない解答になっているか注意して学習しましょう。また、模範解答の解法を使えるようになるためには、注目すべき問題の条件や、他の解法より有効である理由について、思考することが重要です。また、新しく得られた考え方は、本書に取り組み終わった後もたまに見返して忘れないようにしましょう。
【所要時間】162h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。過去問演習前に最難関大学の問題の解法の思考の経験を積むことができるため、最難関ランクの大学で数学を武器にして安定的に合格を狙いたい人向けに採用しました。本書以前に学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学受験の総仕上げとして最適な一冊です。 ③問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。本書は見たことがない解法や問題を経験しておく、ということが目的であるので時間をかけすぎず、他の教科とのバランスを考えながら取り組みましょう。また、本書はレベルが高いため、特に文系の生徒はこの参考書の学習自体が志望大学の合格に必要なのかよく検討してから学習を始めましょう。
【所要時間】65.5h ①演習本 ②本書は他の参考書にないような最難関レベルの問題に触れられる、トップクラスの難易度の問題集です。本改訂により新課程のⅢCに対応し、過去問演習前に最難関大学の問題の解法の思考を十分に練習できる内容となっており、最難関ランクの大学で数学を武器として安定的に合格を狙いたい人向けに採用しました。これまでに学習した知識や考え方を総動員して難問に対処する経験が積めるため、最難関大学の受験の総仕上げとして最適です。最難関ランクの大学の理系の問題では数ⅢCの範囲が合否を分けるので、本書を身につけることができれば数学では確実に合格圏に入ることができるでしょう。 ③本書は理系の最難関レベルの大学を志望する生徒が取り組むので、『文系数学の良問プラチカ』とは違い、標問と同じくらいの練度で取り組みましょう。問題の難易度自体も高いですが、取り組む人が難関ランクの参考書のレベル程度をすでに身につけていることを前提として解説が書かれており親切ではないので、本書までに取り組んだ参考書がきちんと身についていなければ、解説を十分理解することも難しいでしょう。
オプション教材
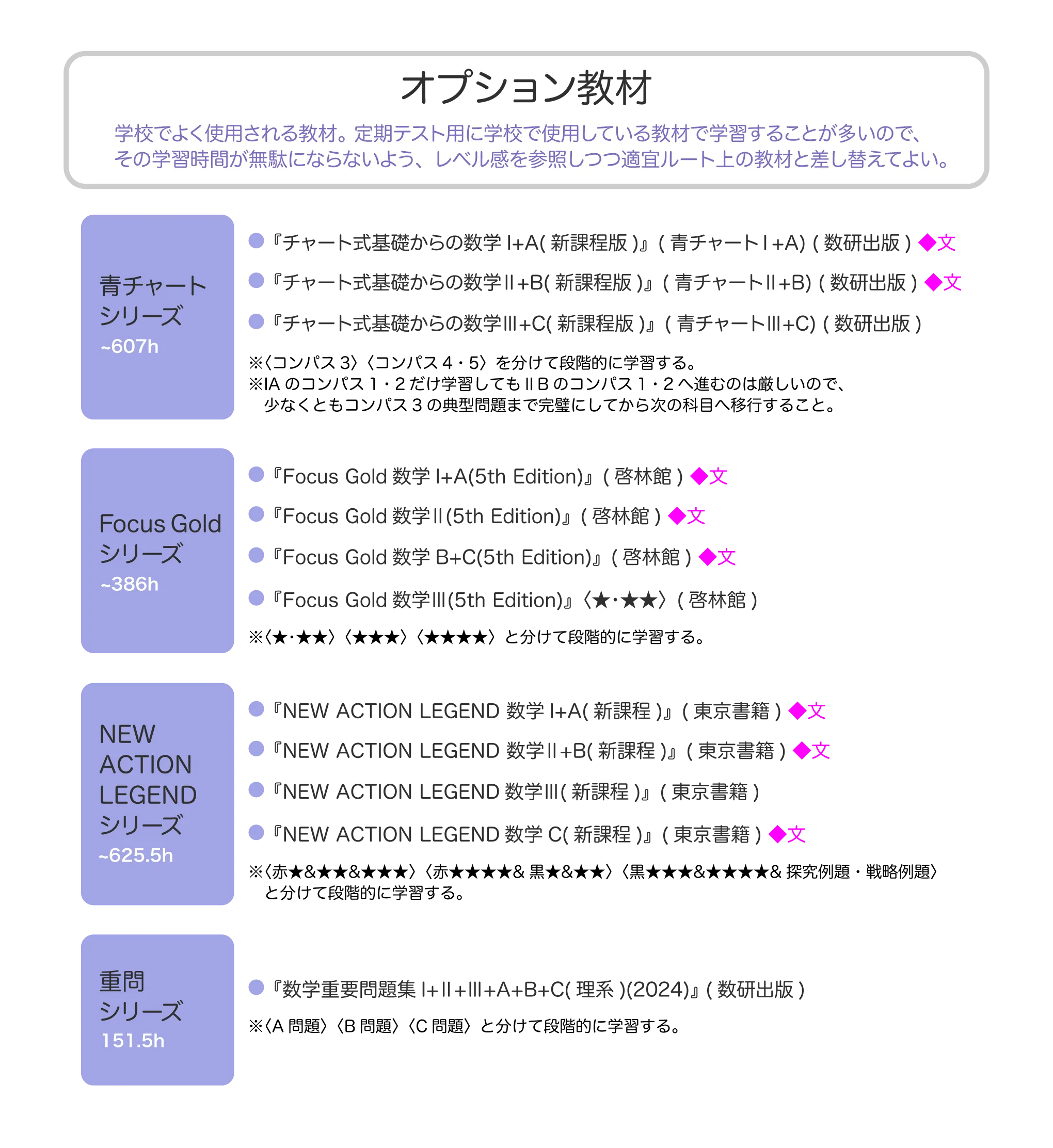
【所要時間】100.5h ①演習本 ②難関大を目指す受験生に対して、解法を一通りインプットするために用います。基本的には本冊子は時短ルートに含まれており、コンパス1・2は扱わない方針ですが、基本的な事項に不安がある場合などではこの部分で基礎事項の確認を行うとよいでしょう。 ③時短ルートに含まれる本冊子は、標準ランクの受験生が利用することを対象としていることから、この部分は基本的にスキップして構いません。
【所要時間】73.5h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。基本例題に加え重要例題も掲載しており、難関大の問題に直結する内容を多く含む構成であるため、典型題を身につけつつ難関大を視野に入れた学習をする生徒向けに採用しました。実際の入試問題で問われる形の典型題を多く収録しているため、典型題に加え、初見の問題に対しどのような思考をして取り組めばよいのか、練習をするのに最適な一冊です。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】22.5h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。実際の難関大の入試問題に触れ、公式や操作の理由をきちんと考えて理解することで、飛躍的な数学力の向上を目指す生徒向けに採用しました。入試問題での問われ方や解法に触れることで、その後の参考書で、ポイントをついた解答の作成や問われやすいパターンの学習がスムーズになるでしょう。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。青チャートのコンパス4・5はかなりレベルが高いため、初めて問題を解く際はどうしても答えを見てしまうことが多くなってしまいますが、解答の暗記はあまり意味がないので、どうして問題文を読んでこの解答にたどり着くのか、思考の過程をよく検討することや数学的な操作の意味を常に理解しながら取り組むことが重要です。
【所要時間】97h ①演習本 ②難関大を目指す受験生に対して、解法を一通りインプットするために用います。基本的には本冊子は時短ルートに含まれており、コンパス1・2は扱わない方針ですが、基本的な事項に不安がある場合などではこの部分で基礎事項の確認を行うとよいでしょう。 ③時短ルートに含まれる本冊子は、標準ランクの受験生が利用することを対象としていることから、この部分は基本的にスキップして構いません。
【所要時間】69h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。基本例題に加え重要例題も掲載しており、難関大の問題に直結する内容を多く含む構成であるため、典型題を身につけつつ難関大を視野に入れた学習をする生徒向けに採用しました。実際の入試問題で問われる形の典型題を多く収録しているため、典型題に加え、初見の問題に対しどのような思考をして取り組めばよいのか、練習をするのに最適な一冊です。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】34h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。実際の難関大の入試問題に触れ、公式や操作の理由をきちんと考えて理解することで、飛躍的な数学力の向上を目指す生徒向けに採用しました。入試問題での問われ方や解法に触れることで、その後の参考書で、ポイントをついた解答の作成や問われやすいパターンの学習がスムーズになるでしょう。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。青チャートのコンパス4・5はかなりレベルが高いため、初めて問題を解く際はどうしても答えを見てしまうことが多くなってしまいますが、解答の暗記はあまり意味がないので、どうして問題文を読んでこの解答にたどり着くのか、思考の過程をよく検討することや数学的な操作の意味を常に理解しながら取り組むことが重要です。
【所要時間】94h ①演習本 ②難関大を目指す受験生に対して、解法を一通りインプットするために用います。基本的には本冊子は時短ルートに含まれており、コンパス1・2は扱わない方針ですが、基本的な事項に不安がある場合などではこの部分で基礎事項の確認を行うとよいでしょう。 ③時短ルートに含まれる本冊子は、標準ランクの受験生が利用することを対象としていることから、この部分は基本的にスキップして構いません。
【所要時間】77h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス3は、すべてのパターンの典型問題を身につけ、この後応用問題に取り組む際の土台となる基礎力を身につける段階です。基本例題に加え重要例題も掲載しており、難関大の問題に直結する内容を多く含む構成であるため、典型題を身につけつつ難関大を視野に入れた学習をする生徒向けに採用しました。実際の入試問題で問われる形の典型題を多く収録しているため、典型題に加え、初見の問題に対しどのような思考をして取り組めばよいのか、練習をするのに最適な一冊です。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。難関ランク・最難関ランクを目指す人は、ただ作業の流れを暗記するのではなく、その作業の意味・目的を理解したうえで、考えずに解けるようになるまで演習してください。
【所要時間】39.5h ①演習本 ②本書は難関大受験生の多くが使う参考書で、網羅性が非常に高い参考書です。すべての例題に解説動画がついており、動画での学習も可能です。コンパス4・5は、コンパス3で身につけた典型問題から初歩の応用問題に進み、実験(条件を満たす解を探す操作)→解法を考える→解答を書く、という実際の入試で行う流れを実際にやってみることで、コンパス3で得た知識を実践的な知識に昇格させる段階になります。実際の難関大の入試問題に触れ、公式や操作の理由をきちんと考えて理解することで、飛躍的な数学力の向上を目指す生徒向けに採用しました。入試問題での問われ方や解法に触れることで、その後の参考書で、ポイントをついた解答の作成や問われやすいパターンの学習がスムーズになるでしょう。 ③チャートは一般的に網羅性が高く、さらに青チャートでは黄チャートより難易度が上がるため、完璧に身につけるのに時間がかなりかかる可能性があります。入試までの時間を検討しよく計画を立てて取り組みましょう。青チャートのコンパス4・5はかなりレベルが高いため、初めて問題を解く際はどうしても答えを見てしまうことが多くなってしまいますが、解答の暗記はあまり意味がないので、どうして問題文を読んでこの解答にたどり着くのか、思考の過程をよく検討することや数学的な操作の意味を常に理解しながら取り組むことが重要です。
【所要時間】48h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。「★・★★」のレベル帯は基本となる問題で構成されており、この部分は問題を見てすぐに答えがかけるぐらいまで仕上げておくことが理想です。 ③本書のこのレベル帯は、一つ前であつかう『やさしい高校数学』と重複している部分があり、本人の学習到達度に応じてスキップして構いません。
【所要時間】51h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は入試において必須となる基礎的な内容がちゃんと盛り込まれており、今後の問題演習を円滑にするためにもこの部分は完璧にしておくことが理想です。 ③このレベル帯をおろそかにしてしまうと、今後の問題演習で引っかかてしまうことが懸念されます。そのため問題を見てすぐ答えを書きだせるほどになるまで完璧にすることを心掛けましょう。
【所要時間】11.5h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は思考力を要する問題が非常に多く、実際の入試問題に近い問題が多く採用されています。解く際には、「なぜその操作で正答にたどり着くのか」などを意識しながら問題に向き合うことを意識しましょう。 ③この辺りから問題の難易度が上がってきて、詰まってしまうことも多くなりますが、すぐに解答をみるのではなく必ず考える時間を取ることを意識しましょう。
【所要時間】32h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。「★・★★」のレベル帯は基本となる問題で構成されており、この部分は問題を見てすぐに答えがかけるぐらいまで仕上げておくことが理想です。 ③本書のこのレベル帯は、一つ前であつかう『やさしい高校数学』と重複している部分があり、本人の学習到達度に応じてスキップして構いません。
【所要時間】43h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は入試において必須となる基礎的な内容がちゃんと盛り込まれており、今後の問題演習を円滑にするためにもこの部分は完璧にしておくことが理想です。 ③このレベル帯をおろそかにしてしまうと、今後の問題演習で引っかかてしまうことが懸念されます。そのため問題を見てすぐ答えを書きだせるほどになるまで完璧にすることを心掛けましょう。
【所要時間】18h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は思考力を要する問題が非常に多く、実際の入試問題に近い問題が多く採用されています。解く際には、「なぜその操作で正答にたどり着くのか」などを意識しながら問題に向き合うことを心掛けましょう。 ③この辺りから問題の難易度が上がってきて、詰まってしまうことも多くなりますが、すぐに解答をみるのではなく必ず考える時間を取ることを意識しましょう。
【所要時間】32.5h ①演習本 ②学校指定で配布されることがおおいことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。「★・★★」のレベル帯は基本となる問題で構成されており、この部分は問題を見てすぐに答えがかけるぐらいまで仕上げておくことが理想です。 ③本書のこのレベル帯は、一つ前であつかう『やさしい高校数学』と重複している部分があり、本人の学習到達度に応じてスキップして構いません。
【所要時間】46.5h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は入試において必須となる基礎的な内容がちゃんと盛り込まれており、今後の問題演習を円滑にするためにもこの部分は完璧にしておくことが理想です。 ③このレベル帯をおろそかにしてしまうと、今後の問題演習で引っかかてしまうことが懸念されます。そのため問題を見てすぐ答えを書きだせるほどになるまで完璧にしましょう。
【所要時間】18h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は思考力を要する問題が非常に多く、実際の入試問題に近い問題が多く採用されています。解く際には、「なぜその操作で正答にたどり着くのか」などを意識しながら問題に向き合うことを意識しましょう。 ③この辺りから問題の難易度が上がってきて、詰まってしまうことも多くなるが、すぐに解答をみるのではなく必ず考える時間を取ることを意識しましょう。
【所要時間】32h ①演習本 ②学校指定で配布されることがおおいことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。「★・★★」のレベル帯は基本となる問題で構成されており、この部分は問題を見てすぐに答えがかけるぐらいまで仕上げておくことが理想です。 ③本書のこのレベル帯は、一つ前であつかう『やさしい高校数学』と重複している部分があり、本人の学習到達度に応じてスキップして構いません。
【所要時間】42.5h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は入試において必須となる基礎的な内容がちゃんと盛り込まれており、今後の問題演習を円滑にするためにもこの部分は完璧にしておくことが理想です。 ③このレベル帯をおろそかにしてしまうと、今後の問題演習で引っかかてしまうことが懸念されます。そのため問題を見てすぐ答えを書きだせるほどになるまで完璧にすることを心掛けましょう。
【所要時間】11h ①演習本 ②学校指定で配布されることが多いことから、学校で配布される参考書を用いたルートに採用します。本書は『チャート式基礎からの数学』(青チャート)とほとんど同じレベル帯です。このレベル帯は思考力を要する問題が非常に多く、実際の入試問題に近い問題が多く採用されています。解く際には、「なぜその操作で正答にたどり着くのか」などを意識しながら問題に向き合うことを意識しましょう。 ③この辺りから問題の難易度が上がってきて、詰まってしまうことも多くなるが、すぐに解答をみるのではなく必ず考える時間を取ることを心掛けましょう。
【所要時間】126.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は非常に基礎的であり、問題を見てすぐに手が動くレベルになるまで繰り返し演習することを推奨します。すでに『やさしい高校数学』などで仕上げている場合は、この部分はスキップしても問題ありません。
【所要時間】13h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は、『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提します。 ③本書のこのレベル帯は数学の根幹となる内容であり、この部分をおろそかにすれば今後の問題演習で支障をきたすため、問題を見てすぐ手が動くレベルになるまで演習を行うことを心掛けましょう。わからない部分はそのままにしておくことなく、すぐに解決するようにしましょう。
【所要時間】64h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。 ③本書のこのレベル帯は難関大の問題も採用されており、思考力を要求する部分が非常に大きいです。そのため、問題を解く際には思考過程に着目して、なぜその解き方で解答にたどり着くのかを常に考えるようにしましょう。
【所要時間】120.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は非常に基礎的であり、問題を見てすぐに手が動くレベルになるまで繰り返し演習することを推奨します。すでに『やさしい高校数学』などで仕上げている場合は、この部分はスキップしても問題ありません。
【所要時間】15.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は数学の根幹となる内容であり、この部分をおろそかにすれば今後の問題演習で支障をきたすため、問題を見てすぐ手が動くレベルになるまで演習を行うことを心掛けましょう。わからない部分はそのままにしておくことなく、すぐに解決するようにしましょう。
【所要時間】69.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は難関大の問題も採用されており、思考力を要求する部分が非常に大きいです。そのため、問題を解く際には思考過程に着目して、なぜその解き方で解答にたどり着くのかを常に考えるようにしましょう。
【所要時間】73.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は非常に基礎的であり、問題を見てすぐに手が動くレベルになるまで繰り返し演習することを推奨します。すでに『やさしい高校数学』などで仕上げている場合は、この部分はスキップしても問題ありません。
【所要時間】15.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は数学の根幹となる内容であり、この部分をおろそかにすれば今後の問題演習で支障をきたすため、問題を見てすぐ手が動くレベルになるまで演習を行うことを心掛けましょう。わからない部分はそのままにしておくことなく、すぐに解決するようにしましょう。
【所要時間】38h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は難関大の問題も採用されており、思考力を要求する部分が非常に大きいです。そのため、問題を解く際には思考過程に着目して、なぜその解き方で解答にたどり着くのかを常に考えるようにしましょう。
【所要時間】57h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は非常に基礎的であり、問題を見てすぐに手が動くレベルになるまで繰り返し演習することを推奨します。すでに『やさしい高校数学』などで仕上げている場合は、この部分はスキップしても問題ありません。
【所要時間】4.5h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は数学の根幹となる内容であり、この部分をおろそかにすれば今後の問題演習で支障をきたすため、問題を見てすぐ手が動くレベルになるまで演習を行うことを心掛けましょう。わからない部分はそのままにしておくことなく、すぐに解決するようにしましょう。å
【所要時間】28h ①演習本 ②学校配布で利用する受験生が多いことから、学校配布の教材を用いたルートに採用します。本書のレベル帯は『チャート式基礎からの数学』(青チャート)や『Focus Gold』に近く、基本的な学習事項は『やさしい高校数学』等で習得済みであることを前提とします。矢印などを豊富に用いて、思考過程を重視した解説が非常に特徴的です。 ③本書のこのレベル帯は難関大の問題も採用されており、思考力を要求する部分が非常に大きいです。そのため、問題を解く際には思考過程に着目して、なぜその解き方で解答にたどり着くのかを常に考えるようにしましょう。
【所要時間】76.5h ①演習本 ②ルートには入っていませんが、時間がない者に向けてオプションとして取り入れています。本書のA問題は入試問題の中でも標準的な問題をメインに扱っており、難関大を目指す生徒にとってはこの部分は完答を目指すことが目標です。時間のない者は、「必解」と書かれたマークの部分だけ選択的に解くことで効率的な学習も可能です。 ③難関大を目指す生徒は、この部分は完解を狙いたいので、解答の段階でミスがあれば必ず解説を熟読して自分のものにすることを意識しましょう。
【所要時間】64h ①演習本 ②ルートには入っていませんが、時間がない者に向けてオプションとして取り入れています。本書のB問題は入試問題の標準からやや難をメインに構成されており、上位国立をねらう受験生はこの辺りまで演習を積んでおきましょう。解答解説を読む際には、なぜその解き方で解答にたどり着くことができるのかをメインに考察することを心掛けましょう。 ③本書の利用は受験に近い時期であることから、解答を作成するときは本番を意識して途中式を丁寧に書くことを心掛けましょう。丁寧に記述することによってミスを減らせることにもつながります。
【所要時間】11h ①演習本 ②ルートには入っていませんが、時間がない者に向けてオプションとして取り入れています。本書のC問題は入試問題のやや難をメインに構成されており、旧帝大、難関大をねらう受験生はこの辺りまで演習を積んでおきましょう。解答解説を読む際には、なぜその解き方で解答にたどり着くことができるのかをメインに考察することを心掛けましょう。 ③本書の利用は受験に近い時期であることから、解答を作成するときは本番を意識して途中式を丁寧に書くことを心掛けましょう。丁寧に記述することによってミスを減らせることにもつながります。
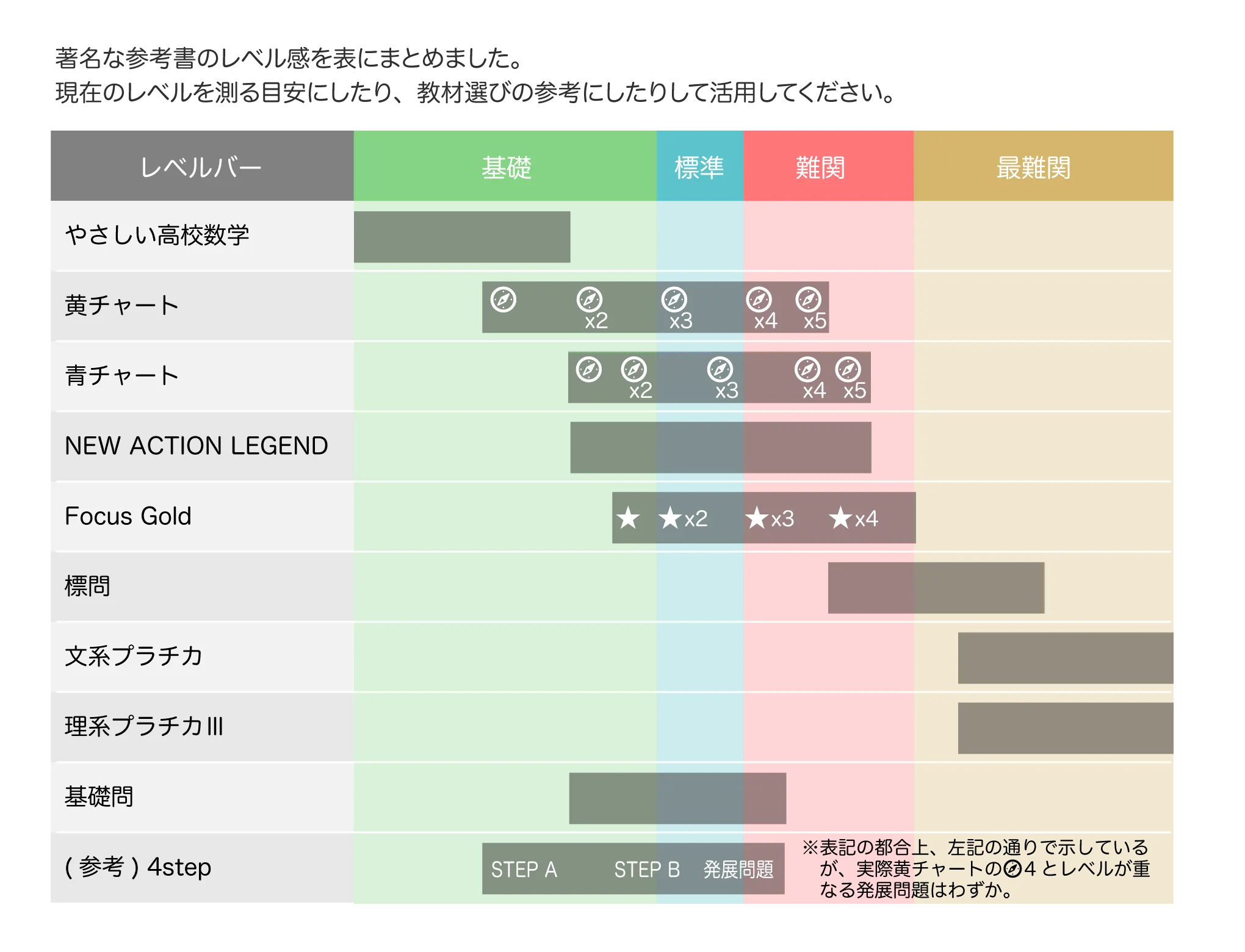
各参考書のレベル
コラム①問題集の時短勉強法
- ×がつく問題なのか〇がつく問題なのかを区別しておく
勉強は×を〇にすることです。すでに〇の問題を繰り返して練習し、〇を重ねようがあまり成長はありません。解いた問題には必ず印をつけておきましょう。参考書で解いた問題以外にも、学校のテストなど他の機会で解いた問題はどの典型題のパターンなのか参考書と見比べて確認し、そのパターンが解けるのか、解けないのかを区別しておきましょう。
- ×の原因を明確にする
《よくある原因》
①方針に欠陥がある(条件の過不足・重複)
②計算等の操作のミス(計算ミス・書きミス)
③論理・記述の欠陥(必要十分の議論不足・記述の丁寧さ不足(特に理系!))
- 原因を修正する
《原因の解決方法》
①自分が考えた方針で答えを合わせきる(調べてよい)・答えが合わない場合は別の方針を探る
:なんとなくで方針を選択しないようにしてください。どうしてその方針がよいのか、悪いのかを考えて理解しないと、問題が解けるかどうかが運頼りになってしまいます。どうしてその方針を選択したのか、問題のどの条件からその方針の選択にいたるのかまで検討しましょう。
②よくミスしやすいポイントと対策を検討する(解答途中にチェックポイントを設定する等)・計算練習
:ケアレスミスとして流してしまうのではなく、自分の間違いやすいポイントをできるだけ具体化してリストアップしましょう。例えば、積分の計算中の原始関数への数値の代入で間違いやすい場合、項が増えると途中で項を飛ばしてしまうなどが原因として上がれば、途中式を増やしπやeなどの特定の文字が含まれる項を先にまとめてその時点で抜けがないか確認する、などできるだけ具体的に対策を考えましょう。また、そもそもの計算練習を増やすことも肝心です。特に理系では計算が大問一問になることもあり、差がつく要因となるので5問でいいので毎日練習するようにしましょう。
③第三者である先生に解答を読んでもらう(自分の解答の読まれ方を知る)
:特に十分性の確認ができていない解答がよく見られます。また、帰納法等で仮定する際に条件が足りていないことも多いです。自分の頭の中で論証の流れができてしまっている場合、解答の不足に気づけないことはよくあります。他の人に見てもらうことで、解答として書かなければいけない条件・根拠などの不足に気づくことができます。
コラム②理系数学と文系数学のポイント
- 文系数学
①できることが限られている文系数学ではうまく工夫して解けるように作業することが大切
②数学が苦手な人が多いので、完答できなくても気づいたことや方針だけでも書いておくだけでアドバンテージになる可能性あり!
- 理系数学
①力技でもいいのでとにかく解ききることが大事なので微積分等の計算練習を絶対に怠らないように
②数Ⅲが多く出題されやすいので一刻も早くⅠAⅡBCを仕上げてⅢに入ろう
③Ⅲは到達度での差が大きいので難しいことが問われにくいので計算練習を固めるだけでアドバンテージを得られる
- 共通すること
学習はⅠ→A→Ⅱ→B(→C)と進めますが、ⅠとAよりⅠとⅡの方が関連が大きいです。模試でⅡの内容で点数が取れない場合は、そもそもⅠで躓いている可能性があります! 躓いた原因を具体的に分析して、穴を埋めましょう。








































